Paper Link: https://www.jmlr.org/papers/volume25/23-0269/23-0269.pdf
Motivation
BO relies on surrogate models (often chosen to be GPs). A GP is specified by a kernel (and a mean sometimes), which reflects our prior knowledge about the black box function of interest. In addition, since we often do not have too many observations being queried from the black box function, the outcome will be sensitive to prior choices.
In this paper, the authors are motivated by BO in the context of hyperparameter tuning of large-scale ML models, where the common choices of the kernel (e.g. SE, Matern) are often unrealistic. In many settings where a GP prior is decided, a lot of domain / contextual knowledge is first gathered to make a sensible guess at how the function might look like (e.g. periodicities, spectral properties, smoothness). Such knowledge is often missing in the ML model hyperparameter tuning case.
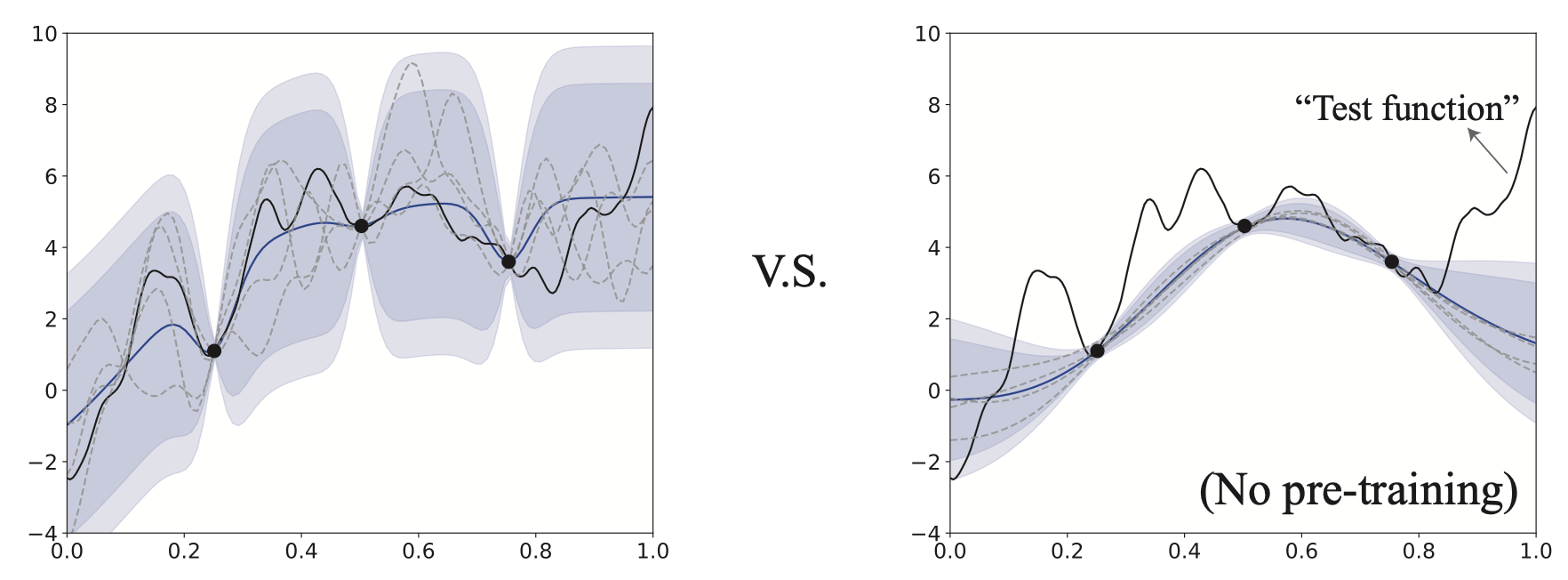
To resolve this issue, the authors proposed a “transfer learning” / “information borrowing” / “pre-training” / “meta-learning” approach to turning existing final GP models from similar large-scale ML models’ hyperparameter tuning tasks into priors for the next task with a slightly different ML model. The new approach is called the HyperBO.
Methods
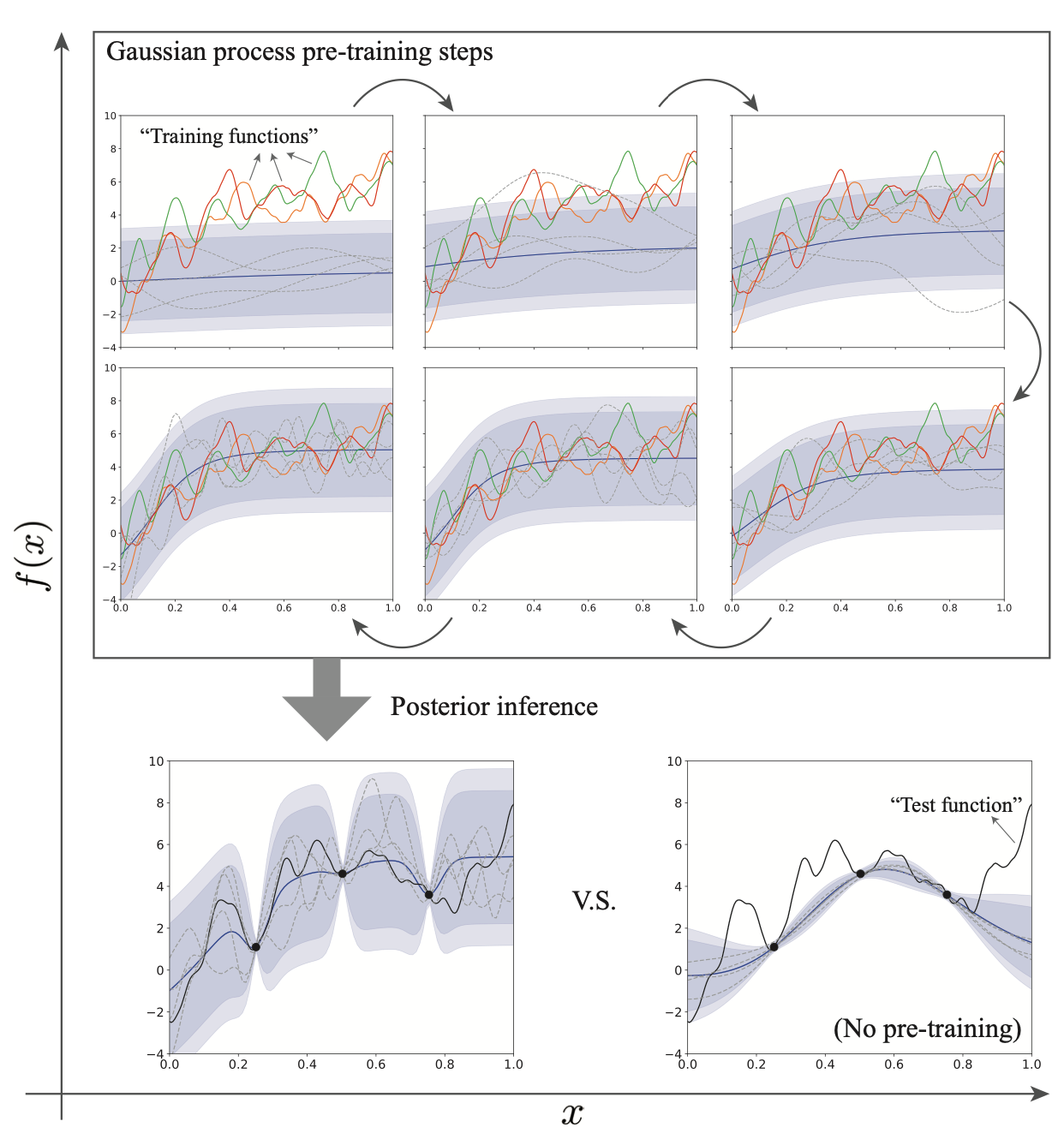
The key component of HyperBO is the construction of a pre-trained prior GP. Everything else goes like the standard BO loops. We denote \(f\)as our current black-box function that we wish to run BO on. We have past knowledge about the functions \(f_1, f_2, \ldots, f_N\) with observation datasets \(D_1, D_2, \ldots, D_N\) each consists of \(M\) location-value pairs of the corresponding function.
The main assumption (Assumption 1 of paper) made in this paper, which is essential for the construction of our pre-trained prior, is that all the previously explored functions as well as our current function are i.i.d. draws from a common meta GP, i.e. \(f_1, f_2, \ldots, f_N, f \sim \mathcal{GP}(\mu^*, k^*)\). The other assumption (Assumption 2), which is more minor, is that the observations are all noisy with noise being additive, centred, Gaussian, and of unknown constant variance \(\sigma_*^2\).
Under these two assumptions, we are ready to explain how the pre-trained prior is obtained. We construct a loss function \(\mathcal{L}\) of the form
\[ \mathcal{L}(\mu, k, \sigma^2)=\text{KL}\left(\mathcal{GP}_{\sigma_*^2}(\mu^*, k^*), \mathcal{GP}_{\sigma^2}(\mu, k)\right) \]
where the subscripts \(\sigma^2, \sigma_*^2\) denote the variances of the observation noise, and this is used to be optimised to obtain our estimations of the hyperparameters of our pre-trained GP. The equation above corresponds to Equation (1) in the paper with slightly adjusted notations.
The paper proposed two ways - KL-based and likelihood-based - to rewrite the above loss function to make it more computationally tractable.
Discussions
The approach proposed in the paper can be (at least intuitively) related to the empirical Bayes approach of inference, where the prior is obtained using some sort of MLEs of the parameters using the observations. Here, the prior GP is modelled as a sample from the meta GP \(\mathcal{GP}(\mu^*, k^*)\) with hyperparameters estimated using existing data of previous BO tasks.
It could also be beneficial to consider the potential link between this work and the generalised Bayes ideas (e.g. A General Framework for Updating Belief Distributions and An Optimization-centric View on Bayes’ Rule). Slightly more concretely, maybe those works could provide a different way of pre-training our GP prior given past observations.
The method proposed in this paper is heavily dependent on the problem setup, especially the Assumption 1 of the paper. This assumption is sensible in many contexts, such as the hyperparameter tuning examples mentioned in the paper, but it is certainly not generally applicable.