step1 = z.reshape(N_A, N_B)
step2 = A @ step1
step3 = step2.T
step4 = B @ step3
result = step4.T.flatten()In this blog post, I will walk through how one could exploit the Kronecker structure of the temporal Gaussian process (GP) regression with one-dimensional space + one-dimensional time inputs and one-dimensional output. This is the second of a series of blog posts on spatial-temporal Gaussian processes.
Separable Kernels
Recall from the last post that we have fitted a temporal GP on an one-dimensional spatial and one-dimensional temporal grid. Since we define the overall kernel as a product of the spatial and temporal component of the kernel, i.e. \(k = k_s \times k_t\), we have the Kronecker structure of the Gram matrices \(K = K_s \otimes K_t\), visually shown below.
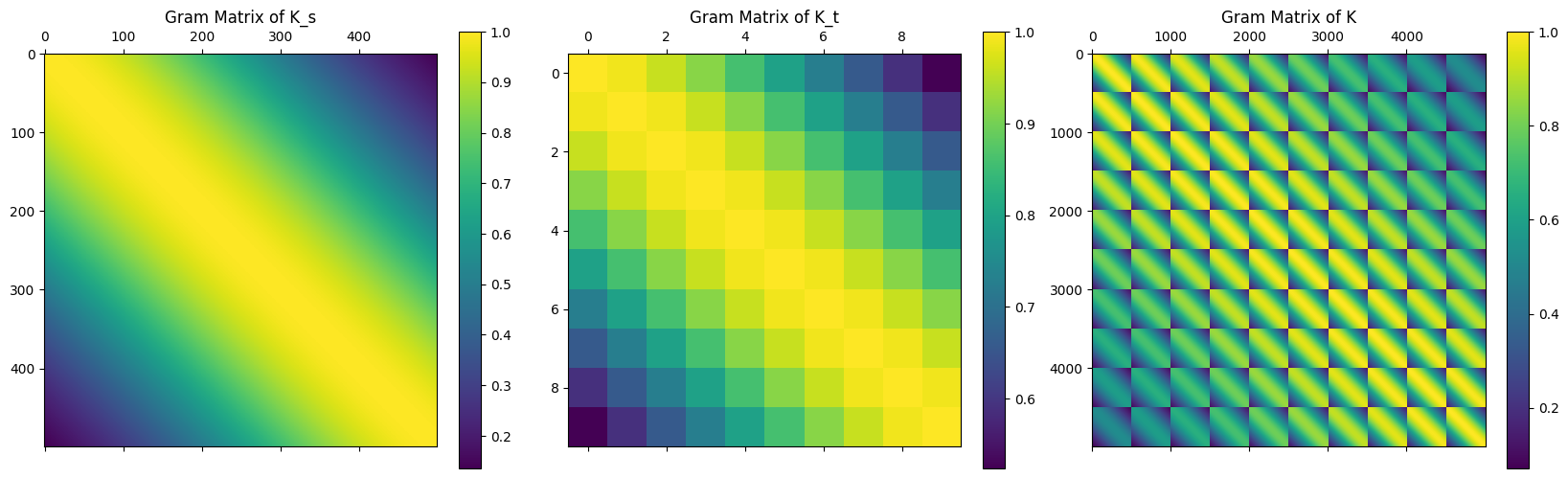
Such kernels are known as separable kernels, and in this post we will explore how one could exploit this structure to obtain significant computational speed ups.
Kronecker Facts
Before describing how one could leverage the Kronecker structure, first we state several relevant and helpful facts about matrices with a Kronecker structure.
Consider two matrices \(A \in \mathbb{R}^{n_1 \times n_2}\), \(B \in \mathbb{R}^{m_1 \times m_2}\). The Kronecker product \(K = A \otimes B \in \mathbb{R}^{n_1 m_1 \times n_2 m_2}\) is defined by
\[ A \otimes B = \begin{bmatrix} a_{11} B & \cdots & a_{1 n_2} B \\ \vdots & \ddots & \vdots \\ a_{n_1 1} B & \cdots & a_{n_1 n_2} B \end{bmatrix}. \]
The Kronecker product operator \(\otimes\) is bi-linear and associative, so we have
\[ \begin{split} A \otimes (B+C) &= A \otimes B + A \otimes C \\ (B+C) \otimes A &= B \otimes A + C \otimes A \\ (k A) \otimes B &= A \otimes (k B) = k (A \otimes B) \\ A \otimes (B \otimes C) &= (A \otimes B ) \otimes C. \\ \end{split} \] More interesting (and relevant here) properties are the ones related to inverse, Cholesky decomposition, and determinant.
First, we have the inverse property
\[ (A \otimes B)^{-1} = A^{-1} \otimes B^{-1} \] for any invertible \(A, B\).
Next, we have the mixed-product property
\[ (A_1 \otimes B_1) (A_2 \otimes B_2) = (A_1 A_2) \otimes (B_1 B_2). \] Note that if we have Cholesky decomposition \(A = LL^*\) for lower triangular matrix \(L\) and its conjugate transpose \(L^*\), we have
\[ A \otimes B = (L_A L_A^*) \otimes (L_B L_B^*) = (L_A \otimes L_B) (L_A^* \otimes L_B^*). \] Similarly, if we have eigendecomposition \(A = Q_A \Lambda_A Q_A^T\) for diagonal matrix \(\Lambda_A\), we have
\[ A \otimes B = (Q_A \Lambda_A Q_A^T) \otimes (Q_B \Lambda_B Q_B^T) = (Q_A \otimes Q_B) (\Lambda_A \otimes \Lambda_B) (Q_A^T \otimes Q_B^T). \]
Finally, if we have square matrices \(A \in \mathbb{R}^{n \times n}\) and \(B \in \mathbb{R}^{m \times m}\), then
\[ | A \otimes B | = | A |^m | B |^n \] for matrix determinants.
Kronecker Matrix-Vector Product
We will first show a useful algorithm to compute matrix-vector product of the form \((A \otimes B) z\) where \(A, B\) are square matrices of size \(N_A \times N_A\) and \(N_B \times N_B\) respectively and \(z \in \mathbb{R}^{N}\) with \(N = N_A N_B\). Note that this algorithm can be generalised to matrix-vector product with matrix being a Kronecker product of \(D\) square matrices.
We will use the \(\operatorname{vec}\) operator where it stacks the columns of a matrix vertically to obtain a single column vector, i.e. for \(A = [a_1, a_2, \ldots, a_k]\) with \(a_i\) being column vectors, we have
\[ \operatorname{vec}(A) = \begin{bmatrix} a_1 \\ \vdots \\ a_k \end{bmatrix}. \]
A property about the \(\operatorname{vec}\) operator and Kronecker product is the following:
\[ (A \otimes B) \operatorname{vec}(Z) = \operatorname{vec}[B Z A^T] = \operatorname{vec}[B (A Z^T)^T] \] Back to the product of interest \((A \otimes B) z\), we have \(z\) as a column vector. To apply the \(\operatorname{vec}\) formula above, we need to reshape \(z\) to enable sensible matrix products. So, we have, using JAX (and JAX Numpy) notations,
where the .reshape in JAX Numpy is practically transpose then reshape - which is also why we transpose before flatten to get the final result. In terms of computational time, the naive implementation of \((A \otimes B) z\) will be \(O( (N_A N_B)^2)\) whereas the Kronecker implementation is only \(O(N_A N_B)\). The Kronecker implementation will be used whenever it is applicable.
Kronecker Matrix-Matrix Product
One could also easily extend the above Kronecker matrix-vector product to Kronecker matrix-matrix product in the following way. Consider the matrix-matrix product \((A \otimes B) Z\) where \(A, B\) are square matrices of size \(N_A \times N_A\) and \(N_B \times N_B\) respectively and \(Z \in \mathbb{R}^{N \times M}\). We will break matrix \(Z\) down in to \(M\) columns and perform Kronecker matrix-vector product to each of the columns. This gives a computational time of \(O(N_A N_B M)\) as opposed to the \(O((N_A N_B)^2M)\) of naive implementation. We could also exploit the vectorisation functionalities to further speed up this product using methods such as jax.vmap.
Standard GP Sampling, Training, and Prediction
For a Gaussian process \(f \sim \mathcal{GP}(\mu, k)\) where \(\mu\) is the mean function and \(k\) is the kernel function, we can draw a sample of \(f\) at test locations \(X_* = (x_1^*, x_2^*, \ldots, x_k^*)\)
\[ f_* = \mu(X_*) + \sqrt{k(X_*, X_*)} ~\xi, \qquad \xi \sim N_k(0, I_k) \] where \(k(X_*, X_*)\) is the Gram matrix and the square root denotes the lower Cholesky factor.
Consider we have made \(m\) observations of this GP \(f\) where the observations are made at locations \(X \in \mathbb{R}^m\) with values \(y \in \mathbb{R}^m\) and the observations are noisy with independent additive Gaussian noise of variance \(\sigma^2\), i.e. \(y = f(X) + \xi\) with \(\xi_i \sim N(0, \sigma^2) ~\forall i = 1, 2, \ldots, m\). Denote the existing observations as \(\mathcal{D} = \{ X, y \}\).
To train the model using data (or conduct MLE1), we need to optimise the log likelihood
\[ \log p(y|X) = - \frac{m}{2}\log(2\pi) - \log | k(X, X) + \sigma^2 I_m | - \frac{1}{2} y ^T ( k(X, X) + \sigma^2 I_m)^{-1} y . \] In addition, we have the (conditional) predictive2 distribution
\[ \begin{split} y_* ~|X_*, \mathcal{D}, \sigma^2 &\sim N_{n}(\mu_{y_* | \mathcal{D}}, K_{y_* | \mathcal{D}}), \\ \mu_{y_* | \mathcal{D}} &= K_*^T (K + \sigma^2 I_n)^{-1} y,\\ K_{y_* | \mathcal{D}} &= K_{**} - K_*^T (K + \sigma^2 I_n)^{-1}K_*. \end{split} \]
which also implies that if we wish to draw a posterior sample we would have
\[ f_* = \mu_{y_* | \mathcal{D}}(X_*) + \sqrt{k_{y_* | \mathcal{D}}(X_*, X_*)} ~\xi, \qquad \xi \sim N_k(0, I_k). \]
“GP Does Not Scale”
It is a consensus / folklore that GP does not scale. This is mostly due to the fact that the training and sampling of GP involves inversions and Cholesky decomposition of \(m \times m\) matrices where \(m\) is the number of observations. Most commonly used algorithms for matrix inversion and Cholesky decomposition are of \(O(m^3)\) time complexity and are serial in natural (so do not enjoy the GPU speed-ups that are prevalent in machine learning) – even a moderately sized data set will induce prohibitive costs.
It is still ongoing research to device tricks and algorithms to make GP more scalable. Some notable approaches includes:
- Inducing Points
- Vecchia Approximations
- SPDE Approach
- Efficiently Posterior Sampling
- Conjugate Gradients.
Here, we will look at one such approach: Kronecker structure exploiting method. Assume we have a 1D space + 1D time temporal GP with \(N_s\) spatial grid points and \(N_t\) temporal grid points. The naive implementation will have a time complexity of \(O((N_s N_t)^3)\), whereas a Kronecker-aware implementation will only have a time complexity of \(O(\max\{N_s, N_t\}^3)\). Below, we will clarify the precise ways we can leverage the matrix structure to achieve computational speed-ups.
Kronecker Product Gaussian Process
The contents here are largely based on Saatchi (2011).
Sampling from a GP
Naive
\[ f_* = \mu(X_*) + \sqrt{K_s \otimes K_t} ~\xi, \qquad \xi \sim N_k(0, I_k) \]
Kronecker
\[ f_* = \mu(X_*) + \left( \sqrt{K_s} \otimes \sqrt{K_t} \right) ~\xi, \qquad \xi \sim N_k(0, I_k) \]
where we can use the Kronecker matrix-vector product.
GP Likelihood
Naive
\[ \log p(y|X) = - \frac{m}{2}\log(2\pi) - \log | K_s \otimes K_t + \sigma^2 I_m | - \frac{1}{2} y^T ( K_s \otimes K_t + \sigma^2 I_m)^{-1}y. \]
Kronecker
There are two places where we need to leverage the Kronecker structure:
- determinant \(| K_s \otimes K_t + \sigma^2 I_m |\)
- inverse \(( K_s \otimes K_t + \sigma^2 I_m )^{-1}\).
Consider eigendecompositions \(K = Q \Lambda Q^T\), \(K_s = Q_s \Lambda_s Q_s^T\), and \(K_t = Q_t \Lambda_t Q_t^T\). We know that \(QQ^T = I\) and \(|Q|=1\), so since
\[ \begin{split} K + \sigma^2 I_m &= Q \Lambda Q^T + Q (\sigma^2 I_m) Q^T = Q (\Lambda + \sigma^2 I_m) Q^T \\ K_s \otimes K_t + \sigma^2 I_m &= (Q_s \otimes Q_t) (\Lambda_s \otimes \Lambda_t + \sigma^2 I_m) (Q_s^T \otimes Q_t^T) \end{split} \]
we have
\[ \begin{split} | K + \sigma^2 I_m | &= |Q| \cdot |\Lambda + \sigma^2 I_m| \cdot |Q^T| = |\Lambda_s \otimes \Lambda_t + \sigma^2 I_m| \\ ( K + \sigma^2 I_m)^{-1} &= Q^{-T} (\Lambda + \sigma^2 I_m)^{-1} Q^{-1} = Q (\Lambda_s \otimes \Lambda_t + \sigma^2 I_m)^{-1} Q^{T} \end{split} \]
where the remaining term \(\Lambda_s \otimes \Lambda_t + \sigma^2 I_m\) is a diagonal matrix, and we can leverage Kronecker matrix-vector (and matrix-matrix) product whenever necessary.